Есть
вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и
садитесь на нее. Где вы сядете — посередине? Или, может быть, с самого
края? Нет, скорее всего, не то и не другое. Вы сядете так, что
отношение одной части скамейки к другой, относительно вашего тела,
будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная...
Садясь на скамейку, вы произвели «золотое сечение». О золотом сечении
знали еще в древнем Египте и Вавилоне, в Индии и Китае. Вели-кий
Пифагор создал тайную школу, где изучалась мистическая суть «золотого
сечения». Евклид применил его, создавая свою геометрию, а Фидий — свои
бессмертные скульптуры. Платон рассказывал, что Вселенная устроена
согласно «золотому сечению». А Аристотель нашел соответствие «золотого
сечения» этическому закону. Высшую гармонию «золотого сечения» будут
проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое
сечение» — это одно и то же. А христианские мистики будут рисовать на
стенах своих монастырей пентаграммы «золотого сечения», спасаясь от
Дьявола. При этом ученые — от Пачоли до Эйнштейна — будут искать, но
так и не найдут его точного значения. Бесконечный ряд после запятой —
1,6180339887... Странная, загадочная, необъяснимая вещь: эта
божественная пропорция мистическим образом сопутствует всему живому.
Неживая природа не знает, что такое «золотое сечение». Но вы непременно
увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и
в облике жуков, и в красивом человеческом теле. Все живое и все
красивое — все подчиняется божественному закону, имя которому —
«золотое сечение». Так что же такое «золотое сечение»?.. Что это за
идеальное, божественное сочетание? Может быть, это закон красоты? Или
все-таки он — мистическая тайна? Научный феномен или этический принцип?
Ответ неизвестен до сих пор. Точнее — нет, известен. «Золотое сечение»
— это и то, и другое, и третье. Только не по отдельности, а
одновременно... И в этом его подлинная загадка, его великая тайна.
Феномен
золотого сечения известен человечеству очень давно.
Его
тайну пытались осмыслить Платон, Евклид, Пифагор, Леонардо да Винчи,
Кеплер и многие другие крупнейшие мыслители человечества. Они неразрывно
связывали золотое сечение с понятием всеобщей гармонии, пронизывающей
вселенную от микромира до макрокосмоса.
Классическими
проявлениями золотого сечения являются предметы обихода, скульптура
и архитектура [1, 2, 3, 4, 5], математика [6, 7, 8], музыка [9 10,
11] и эстетика [12, 13, 14, 15, 16]. В предыдущем столетии с расширением
области знаний человечества резко увеличилось количество сфер, где
наблюдается феномен золотой пропорции. Это биология и зоология [17,
18, 19], экономика [20, 21], психология [22, 23, 24], кибернетика
[7, 25], теория сложных систем [26, 27], и даже геология [28, 29]
и астрономия [30].
Ежегодно
издаются несколько книг посвященных этой проблеме, постоянно расширяя
область приложения золотого сечения. Авторы этих исследований связывают
золотое сечение с такими несовместимыми, на первый взгляд понятиями,
как красота, асимметрия, рекурсия, самоорганизация и пропорция.
За последние годы появились интересные интернет-сайты [31, 32, 33]
посвященные золотому сечению.
По
глубокому убеждению автора, живая природа построена на простых принципах
и может быть описана элементарными моделями. В этой статье автор
сделает попытку системного анализа феномена золотого сечения и выскажет
несколько предположений, позволяющих объяснить всеобщий характер
золотой пропорции.
Самоподобность и асимметрия
В основе
организации живой материи лежат принципы устойчивости, самоорганизации
и саморегулирования. В формообразовании эти принципы проявляются
как самоподобность. Самоподобность, мы будем понимать, как некоторую
рекурсивную процедуру, порождающую связанную систему объектов.
Ярким примером таких систем являются фракталы [38], получаемые как
рекурсивные геометрические преобразования. Многие объекты живой
природы имеют ярко выраженную фрактальную структуру. Например: деревья,
морская капуста, легкие и кровеносные сосуды человека, и другие.
| Рассмотрим
геометрическую аналогию самоподобности – «динамический» прямоугольник
с отношением сторон равным α. Самоподобность
выражается в том, что присоединяя к большей стороне «динамического»
прямоугольника ABCD (рис 3) квадрат DCFE со стороной, равной
этой стороне, получим прямоугольник ABFE , подобный первоначальному.
Аналогично, если отсечь от «динамического» прямоугольника ABCD
квадрат AMND , то получим прямоугольник MBCN подобный «динамическому».
Нетрудно доказать, что «динамический» прямоугольник
может иметь соотношение сторон только равное α.
|
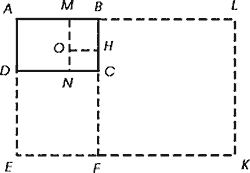 Рис.
3
Рис.
3 |
Операцию
отсечения или добавления квадрата можно производить многократно, и
в результате всегда будет получаться прямоугольник с соотношением
сторон равным α. «Динамический» прямоугольник
также называют «живым». Присоединяя к "живому" прямоугольнику
"неживую" фигуру квадрат, получим опять "живую".
Это аналогия экспансии биологической жизни на окружающее пространство.
Эта модель содержит в себе не только самоподобность, но и асимметрию.
Под асимметрией, мы будем понимать не отсутствие симметрии, а некоторое
нарушение ее.
В
квадрате, симметричной фигуре, все стороны равны, а в «динамическом»
прямоугольнике стороны равны лишь попарно.
По
мнению основателя синергетики Г. Хагена [27], появление асимметрии
вызывает понижение степени симметрии пространства, которое является
необходимым условием самоорганизации, что приводит к появлению внутренних
сил, являющихся основой саморегуляции.
Так,
«неживая» фигура квадрат имеет 4 оси симметрии, а “динамический” прямоугольник
только две.
Пентагональная симметрия и асимметрия
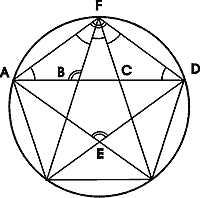 Рис.
4
Рис.
4 |
|
Пентагональная
симметрия встречается только в живой природе и является отличительной
чертой саморегулирующихся систем. Тогда как в кристаллах – «неживых
структурах», согласно классической кристаллографии, возможны симметрии
третьего, четвертого и шестого порядков [39]. В отличии от классических
кристаллов, квазикристаллы 5-го порядка, открытые Дэном Шехтманом
являются "пограничными" объектами на стыке "живого"
и "неживого". Чем глубже мы будем понимать разницу между
"живым" и "неживым", тем больше мы будем находить
"пограничных" объектов. Из всех правильных фигур только
пятиугольником нельзя заполнить плоскость. То есть, из них нельзя
выложить паркет.
Нужно отметить, что в поперечном сечении двойная спираль ДНК -
правильный пятиугольник [40, 41].
Золотое
сечение на прямой и пентагональная симметрия на плоскости являются
отображением внутренней асимметрии самоподобных систем.
Золотое сечение в живописи

Портрет
Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей,
которые обнаружил, что композиция рисунка основана на золотых
треугольниках, являющихся частями правильного звездчатого
пятиугольника. Существует очень много версий об истории этого портрета.
Вот одна из них. Однажды Леонардо да Винчи получил заказ от банкира
Франческо де ле Джокондо написать портрет молодой женщины, жены
банкира, Монны Лизы. Женщина не была красива, но в ней привлекала
простота и естественность облика. Леонардо согласился писать портрет.
Его модель была печальной и грустной, но Леонардо рассказал ей сказку,
услышав которую, она стала живой и интересной.

Золотое сечение в математике
В
математике пропорцией (лат. proportio) называют равенство двух
отношений: a : b = c : d.Отрезок прямой АВ можно разделить на две части
следующими способами:
* на две равные части – АВ : АС = АВ : ВС;
* на две неравные части в любом отношении (такие части пропорции не образуют);
* таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое
сечение – это такое пропорциональное деление отрезка на неравные части,
при котором весь отрезок так относится к большей части, как сама
большая часть относится к меньшей; или другими словами, меньший отрезок
так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.

Ряд Фибоначчи
С
историей золотого сечения косвенным образом связано имя итальянского
математика монаха Леонардо из Пизы, более известного под именем
Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил
Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его
математический труд «Книга об абаке» (счетной доске), в котором были
собраны все известные на то время задачи. Одна из задач гласила
«Сколько пар кроликов в один год от одной пары родится». Размышляя на
эту тему, Фибоначчи выстроил такой ряд цифр:
Ряд чисел 0, 1, 1,
2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи.
Особенность последовательности чисел состоит в том, что каждый ее член,
начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5
+ 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел
ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а
34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это
отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в
золотой пропорции, увеличение его или уменьшение до бесконечности,
когда меньший отрезок так относится к большему, как больший ко всему.
Последовательность чисел 1,1,2,3,5,8,13,21,...,
называемая числами Фибоначчи и образуемая по рекуррентной формуле:
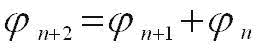 (4)
(4)
где
n - натуральное число и начальные члены равны 1 и 1.
Ярким
примером проявления чисел Фибоначчи в живой природе является филлотаксис
[19].Французский математик Бине показал, как связаны числа Фибоначчи
и основание золотой пропорции:
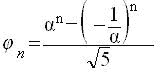 (5)
(5)
Эта формула интересна тем, что справа находятся иррациональные числа
α
и 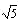 , а слева всегда целое.
Нужно отметить асимметричность знаменателя правой части формулы
5. Из последней формулы легко получить следующее соотношение : , а слева всегда целое.
Нужно отметить асимметричность знаменателя правой части формулы
5. Из последней формулы легко получить следующее соотношение :
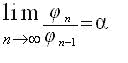 (6)
(6)
которое
вместе с формулами 2, 4 и 5 показывает глубокую связь между числами
Фибоначчи и основанием золотой пропорции. В формулах 1, 3, 5 можно
заметить почти «мистическое» присутствие числа 5.
Если
в рекурсивной последовательности образуемой по формуле 4, задать
произвольные начальные члены, то предел отношения двух соседних
членов этого ряда все равно будет стремиться к α (формула
6). Даже некоторое количество арифметических ошибок в вычислении
φi при 1<i<<n,
не повлияют на этот результат.
Основание
золотой пропорции является инвариантом рекурсивных соотношений 4
и 6. В этом проявляется «устойчивость» золотого сечения, одного
из принципов организации живой материи
Так
же, основание золотой пропорции является решением двух экзотических
рекурсивных последовательностей
Присутствие
золотой пропорции и чисел Фибоначчи в живой природе позволяют говорить
о некотором едином механизме их возникновения.
Числа
Фибоначчи и золотое сечение являются математическим описанием некоторого
формообразующего процесса. На микроуровне (целочисленном) количественная
характеристика этого процесса проявляется как числа Фибоначчи, а
на макроуровне (статистическом) как основание золотой пропорции
- число α.
Если
такой формообразующий процесс является законом живой природы, то
с его помощью можно объяснить наличие золотой пропорции в соотношении
частей тела человека и животных, а также явление филлотаксиса.
Золотое сечение в биологии

В
биологических исследованиях 70-90 гг. показано, что, начиная с вирусов
и растений и кончая организмом человека, всюду выявляется золотая
пропорция, характеризующая соразмерность и гармоничность их строения.
Золотое сечение признано универсальным законом живых систем. Можно
отметить два вида проявлений золотого сечения в живой природе:
иррациональные отношения по Пифагору - 1.62 и целочисленные, дискретные
- по Фибоначчи.
Было установлено, что числовой ряд чисел
Фибоначчи характеризует структурную организацию многих живых систем.
Например, винтовое листорасположение на ветке составляет дробь (число
оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13),
соответствующую рядам Фибоначчи. Хорошо известна "золотая" пропорция
пятилепестковых цветков яблони, груши и многих других растений.
Носители генетического кода - молекулы ДНК и РНК - имеют структуру
двойной спирали; ее размеры почти полностью соответствуют числам ряда
Фибоначчи.
Анатомия
Золотое сечение можно найти и
в анатомии. Закон золотого сечения просматривается в количественном
членении человеческого тела, соответствующем числам ряда Фибоначчи.
Примером может быть число костей туловища, черепа и конечностей. Так, в
скелете туловища различают 3 костных системы: позвоночник, реберный его
отдел и грудину. Грудина включает 3 кости (рукоятку, тело и мечевидный
отросток). Позвоночник состоит из 33 (34) позвонков; от них отходят
12-13 пар ребер.
Мозговой череп состоит из 8 костей. В верхней и
нижней челюстях с каждой стороны имеется по 8 альвеол и соответственно
- корни 8 зубов.
Скелет верхней конечности состоит из 3 частей
(плечевой, костей предплечья и костей кисти). Кисть включает 8 костей
запястья, 5 пястных костей и кости 5 пальцев. Каждый палец, кроме
большого, имеет по 3 фаланги. Таким образом, морфогенез кисти,
включающей два соседних члена числового ряда Фибоначчи - в частности, 8
костей запястья и 5 костей пясти - приближается к золотому сечению
1.618, поскольку 8/5=1.6.
Сопоставляя длины фаланг пальцев и
кисти руки в целом, а также расстояния между отдельными частями лица,
также можно найти "золотые" соотношения:

Золотое
сечение присутсвует вовсем что нас окружает, природа создает мир вокруг
нас по своим законам, но и эти законы "подвержены" правилу золотого
сечения.
Асинхронное деление клеток
В биологии
существует понятие, называемое асинхронным делением (дроблением).
В монографии К.Г. Газаряна и Л.В. Белоусова "Биология индивидуального
развития животных" [42] автор нашел: "Начиная с 11-го
деления, дробление становится повсеместно асинхронным", там
же, "В яйцах многих групп животных - круглых червей, некоторых
моллюсков, млекопитающих - периода синхронных делений нет: начиная
со 2-го деления, дробление идет асинхронно".
При
асинхронном делении каждая клетка делится на две клетки, одна из
которых пропускает следующий такт деления. Для
краткости, такой формообразующий процесс будем называть F-делением.
| Рассмотрим
количественные характеристики F-деления. После определенного
количества синхронных делений происходят исключительно F-деления.
Так после первого такта F-деления образуются две клетки А и
В (рис 5), из которых только В будет делиться во втором такте.
После двух тактов F-деления образуются три клетки, из которых
только две будут делиться в третьем такте. После третьего такта
суммарное количество клеток станет равным пяти, из которых три
будут делиться в четвертом такте F-деления и т.д. Следовательно,
в процессе F-деления из одной клетки будет образовываться 2,3,5,8,13,21,..
клеток. |
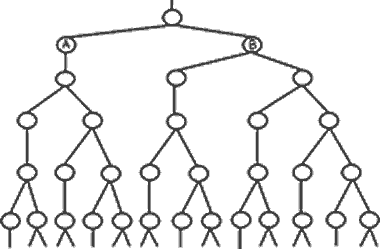 Рис.
5
Рис.
5 |
Гипотеза
о F-делении клеток позволяет объяснить наличие золотой пропорции
в результатах исследований из раздела 3, сердечных ритмах человека
[43, 44], а также в линейных размерах тела человека, например руки
(Рис. 2).
Пусть
на определенном этапе развития зародыша, после периода синхронных
делений, выделится одна клетка из которой будет развиваться рука.
После первого F-деления образуются две клетки А и В (рис 5). Клетка
А пропустит следующий такт деления, следовательно, ее потомков будет
в ? раз меньше клеток потомков В. Действительно, как видно из рисунка
1 отношение длины кисти и локтя к предплечью есть золотое сечение.
Принимая длину, пропорциональной количеству клеток, получаем, что
из клетки А будет развиваться предплечье, а из В кисть и локоть.
Аналогично после деления В, из образовавшихся дочерних клеток, будут
развиваться локоть и кисть, и т.д. до фаланг пальцев на руке.
Граф
на рисунке 5 не является оригинальным, похожие рисунки можно увидеть
при решении задач о росте деревьев, размножении кроликов и пчел
[45], а также на предложенной британским эмбриологом C. H. Waddington
[46] схеме прогрессивного назначения эмбриональных клеток.
Нетрудно
заметить, что Граф на рисунке 5 является фрактальной структурой.
| |
9. Асинхронность, асимметрия и диалектика
Предположение 9
Асинхронность есть выражение асимметричности во
времени.
При F-делении происходит уменьшение количества
осей симметрии образующейся совокупности клеток, что является необходимым
условием самоорганизации по Хагену [27].
Предположение
10
Асимметричность
морфологических процессов является источником внутреннего противоречия,
необходимым условием возникновения и существования самоорганизующихся
систем.
В
F-делении клеток с одной стороны, присутствует симметрия - каждая
клетка делится на две, с другой стороны, после деления клетки не
равноправны - асимметрия.
Симметрия
и асимметрия являются диалектическими противоположностями.
Предположение
11
Диалектическое
противоречие между симметрией и асимметрией является движущей силой
саморегуляции.
Гегель
писал: «Противоречие - корень всего движения и живучести» [48].
Перефразируя известный философский закон «О Единстве Противоположностей»,
получим закон «О Единстве Симметрии и Асимметрии».
Белорусский
философ Э.М.Сороко высказал предположение, что «сочетание симметрии
и асимметрии в определенной пропорции и есть гармония» [26]. |
|
10. Морфологические процессы и асимметрия
Предположение 12
Асимметричность морфологических процессов есть фундаментальный
закон живой материи, а числа Фибоначчи, золотое сечение и пентагональная
симметрия его количественное отображение.
Приведенные выше предположения дают возможность
качественно нового подхода к изучению живой материи.
Становится
возможным построение реальных математических моделей живых организмов
и всевозможных самоорганизующихся систем.
|
|